(长期持续更新)cs61a入门算法记录

发表于 2023/11/19 更新于 2023/11/25

作者 mordecaimaic 15 分钟阅读

CS61a入门算法记录

本文长期记录一些，我认为在cs61a中让我耳目一新的算法

week1

Todo

week2

Todo

week3

Todo

week4

Todo

week5

count_stair_ways

这个算法要求是，如果有n个台阶，每次可以走一步或者两步，那么要求出多少种走法

  
  def count_stair_ways(n):
  """Returns the number of ways to climb up a flight of
  n stairs, moving either one step or two steps at a time.
  >>> count_stair_ways(1)
  1
  >>> count_stair_ways(2)
  2
  >>> count_stair_ways(4)
  5
  """
  "*** YOUR CODE HERE ***"
  if n == 1:
      return 1
  elif n == 2:
      return 2
  else:
      return count_stair_ways(n - 1) + count_stair_ways(n - 2)

count_k

这个算法要求是上面的算法的进阶，假设n是台阶的数量，k是每次可以走的最大步数，那么要求计算出有多少种走法。

def count_k(n, k):
  """Counts the number of paths up a flight of n stairs
  when taking up to k steps at a time.
  >>> count_k(3, 3) # 3, 2 + 1, 1 + 2, 1 + 1 + 1
  4
  >>> count_k(4, 4)
  8
  >>> count_k(10, 3)
  274
  >>> count_k(300, 1) # Only one step at a time
  1
  """
  "*** YOUR CODE HERE ***"
  if n == 0:
      return 1
  elif n < 0:
      return 0
  else:
      total = 0
      for i in range(1, k + 1):
          total += count_k(n - i, k)
      return total

count_k解析

这个函数的目标是计算爬上一个有 n 阶的楼梯有多少种方法，如果你一次可以爬 1 到 k 阶。这个函数的工作方式是使用了一种叫做递归的技术。以下是这个函数的详细解释：

函数定义：def count_k(n, k): 这一行定义了函数的名字（count_k）和它接受的两个参数（n 和 k）。n 是楼梯的阶数，k 是你一次可以爬的最大阶数。
基本情况：if n == 0: 和 elif n < 0: 这两行处理了两种基本情况。如果 n 等于 0，那么说明你已经到达了楼顶，所以有 1 种方法可以到达（也就是不需要再爬）。如果 n 小于 0，那么说明你试图一次爬过多的阶数，这是不可能的，所以有 0 种方法可以到达。
递归调用：for i in range(1, k + 1): 这一行开始了一个循环，对于每一个 i（从 1 到 k），我们都计算有多少种方法可以爬上剩下的 n - i 阶。这是通过递归调用 count_k(n - i, k) 来实现的。
计算总的方法数：total += count_k(n - i, k) 这一行把每一种可能的爬法的方法数加到 total 上。这样，total 就会包含所有可能的爬法的方法数。
返回结果：return total 这一行返回了总的方法数。这就是这个函数的结果。

这个函数的关键在于理解递归的思想。我们从一个大问题开始，然后将其分解成更小的问题，然后解决这些小问题。这就是这个函数的基本思想。

count_k例子

让我们来看看 count_k(3, 3) 是如何工作的。

首先，我们要计算爬上3阶楼梯有多少种方法，如果我们一次可以爬1、2或3阶。

我们首先考虑一次爬1阶的情况。如果我们首先爬1阶，那么我们需要计算爬上剩下的2阶楼梯有多少种方法。这就变成了一个新的问题 count_k(2, 3)。
然后，我们考虑一次爬2阶的情况。如果我们首先爬2阶，那么我们需要计算爬上剩下的1阶楼梯有多少种方法。这就变成了一个新的问题 count_k(1, 3)。
最后，我们考虑一次爬3阶的情况。如果我们首先爬3阶，那么我们已经到达了楼顶，所以这种情况下有1种方法。
我们把所有这些方法加起来，就得到了总的方法数。所以，count_k(3, 3) 的结果是 count_k(2, 3) + count_k(1, 3) + 1。
而 count_k(2, 3) 的结果是 count_k(1, 3) + count_k(0, 3) + count(-1, 3)。
按照此种方法以此类推，得到最终的答案。

这就是 count_k(3, 3) 的工作原理。这个函数的关键在于理解递归的思想。我们从一个大问题开始，然后将其分解成更小的问题，然后解决这些小问题。这就是这个函数的基本思想。

如果学习过cs50的话，在tideman这个作业里面，应该就使用过这种方法，递归+for循环迭代。

paths

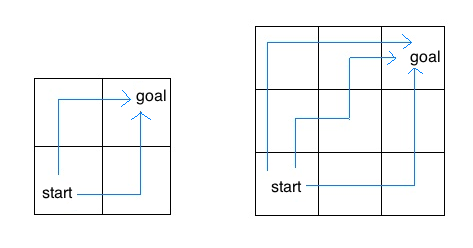
这个算法要求是找到从左上角到右下角的所有路径的数量。假设有一个m*n的网格，从最左下角(start)开始到最右上角(goal)结束，每次只能向右或者向上移动一格，那么有多少种不同的路径可以到达end。

  
  def paths(m, n):
    """Return the number of paths from one corner of an
    M by N grid to the opposite corner.

    >>> paths(2, 2)
    2
    >>> paths(5, 7)
    210
    >>> paths(117, 1)
    1
    >>> paths(1, 157)
    1
    """
    "*** YOUR CODE HERE ***"
    if m == 1 and n == 1:
        return 1
    elif m == 1:
        return paths(m, n - 1)
    elif n == 1:
        return paths(m - 1, n)
    else:
        return paths(m - 1, n) + paths(m, n - 1)

max_product

这个算法要求是，给定一个list，找到list中的最大乘积，但是不能有连续(下表的index不能够连续)的元素。

例如在[10,3,1,9,2]中，最大的乘积是10*9=90

  
def max_product(s):
    """Return the maximum product that can be formed using
    non-consecutive elements of s.
    >>> max_product([10,3,1,9,2]) # 10 * 9
    90
    >>> max_product([5,10,5,10,5]) # 5 * 5 * 5
    125
    >>> max_product([])
    1
    """
    def helper(s, i):
            if i >= len(s):
                return 1
            else:
                # Either include s[i] in the product and skip s[i + 1]
                include = s[i] * helper(s, i + 2)
                # Or exclude s[i] from the product and consider s[i + 1]
                exclude = helper(s, i + 1)
                print(include, exclude)
                return max(include, exclude)

    return helper(s, 0)

max_product解析

这段代码的目标是找出数组中非连续元素的最大乘积。

这个函数 max_product 有一个内部函数 helper，它接受一个数组 s 和一个索引 i，并返回从索引 i 开始的子数组中非连续元素的最大乘积。

对于每个元素 s[i]，我们有两种选择：

包含 s[i] 在乘积中，然后跳过 s[i + 1]。这种情况的乘积是 s[i] * helper(s, i + 2)。
不包含 s[i] 在乘积中，然后考虑 s[i + 1]。这种情况的乘积是 helper(s, i + 1)。

我们选择这两种情况中的最大值作为结果。

最后，我们从索引 0 开始调用 helper 函数，也就是从数组的开始处开始计算最大乘积。

这就是这段代码的基本工作原理。

max_product例子

以下是 max_product([10,3,1,9,2]) 的递归调用树：

max_product([10,3,1,9,2])
├── 10 * max_product([1,9,2])   # 包含10
│   ├── 1 * max_product([2])   # 包含1
│   │   ├── 2 * max_product([])   # 包含2
│   │   └── max_product([])   # 不包含2
│   └── max_product([9,2])   # 不包含1
│       ├── 9 * max_product([])   # 包含9
│       └── max_product([2])   # 不包含9
│           ├── 2 * max_product([])   # 包含2
│           └── max_product([])   # 不包含2
└── max_product([3,1,9,2])   # 不包含10
    ├── 3 * max_product([9,2])   # 包含3
    │   ├── 9 * max_product([])   # 包含9
    │   └── max_product([2])   # 不包含9
    │       ├── 2 * max_product([])   # 包含2
    │       └── max_product([])   # 不包含2
    └── max_product([1,9,2])   # 不包含3
        ├── 1 * max_product([2])   # 包含1
        │   ├── 2 * max_product([])   # 包含2
        │   └── max_product([])   # 不包含2
        └── max_product([9,2])   # 不包含1
            ├── 9 * max_product([])   # 包含9
            └── max_product([2])   # 不包含9
                ├── 2 * max_product([])   # 包含2
                └── max_product([])   # 不包含2

在这个树中，每个节点都表示一个递归调用。节点的子节点表示在该步骤中可能的下一步。例如，max_product([10,3,1,9,2]) 的子节点是 10 * max_product([1,9,2]) 和 max_product([3,1,9,2])，这表示我们可以选择包含 10 或者不包含 10。

请注意，当数组为空时，我们返回 1，因为这表示我们已经考虑了所有的元素。

flatten

这个算法要求是，利用递归，用flatten函数将一个无限多层多层嵌套的list转换成一个一维的list。例如将深层列表[ 1, [[2], 3], 4, [5, 6]]，转换为[1, 2, 3, 4, 5, 6]。

我的solution

我的解法有有点复杂并且有一点重复性，但是我觉得这个解法是我自己想出来的，所以就记录下来了。大概的思路就是定义一个辅助函数flatten_element，和原来的的flatten函数进行互相递归调用。

  
def flatten(s):
    """Returns a flattened version of list s.

    >>> flatten([1, 2, 3])
    [1, 2, 3]
    >>> deep = [1, [[2], 3], 4, [5, 6]]
    >>> flatten(deep)
    [1, 2, 3, 4, 5, 6]
    >>> deep                                # input list is unchanged
    [1, [[2], 3], 4, [5, 6]]
    >>> very_deep = [['m', ['i', ['n', ['m', 'e', ['w', 't', ['a'], 't', 'i', 'o'], 'n']], 's']]]
    >>> flatten(very_deep)
    ['m', 'i', 'n', 'm', 'e', 'w', 't', 'a', 't', 'i', 'o', 'n', 's']
    """
    "*** YOUR CODE HERE ***"
    
    if type(s) != list:
        return [s]
    elif len(s) == 1:
        return flatten_element(s[0])
    else:
        return flatten_element(s[0]) + flatten(s[1:])

def flatten_element(element):
    if type(element) != list:
        return [element]
    else:
        return flatten(element)

gpt的解法

copilot的解法非常简洁高效

  
def flatten_copilot(s):
    """Returns a flattened version of list s.

    >>> flatten([1, 2, 3])
    [1, 2, 3]
    >>> deep = [1, [[2], 3], 4, [5, 6]]
    >>> flatten(deep)
    [1, 2, 3, 4, 5, 6]
    >>> deep                                # input list is unchanged
    [1, [[2], 3], 4, [5, 6]]
    >>> very_deep = [['m', ['i', ['n', ['m', 'e', ['w', 't', ['a'], 't', 'i', 'o'], 'n']], 's']]]
    >>> flatten(very_deep)
    ['m', 'i', 'n', 'm', 'e', 'w', 't', 'a', 't', 'i', 'o', 'n', 's']
    """
    if type(s) != list:
        return [s]
    else:
        result = []
        for element in s:
            result += flatten(element)
        return result

代码解释

GitHub Copilot: 这段代码的目标是将一个可能包含嵌套列表的列表 “flatten”，也就是将所有的元素放入一个单一的列表中。这是一个常见的问题，通常可以通过递归来解决。

这个 flatten_copilot 函数接受一个参数 s，这个参数可以是任何类型的值，但我们主要关注的是列表类型的值。

首先，我们检查 s 是否是列表类型。如果不是，我们将 s 包装在一个列表中并返回。这是递归的基本情况，也就是我们知道如何直接处理的情况。
如果 s 是一个列表，我们创建一个空列表 result，用于存储 “flattened” 的元素。
然后，我们遍历 s 中的每个元素。对于每个元素，我们递归地调用 flatten_copilot 函数。这个递归调用会返回一个 “flattened” 的列表，我们使用 += 操作符将其添加到 result 中。
最后，当我们处理完 s 中的所有元素后，我们返回 result。这个 result 就是 “flattened” 的 s。

这就是这段代码的基本工作原理。通过递归，我们能够处理任意深度的嵌套列表。

CS自学, CS 61A

cs61a

本文由作者按照 CC BY 4.0 进行授权

CS61a入门算法记录

week1

week2

week3

week4

week5

count_stair_ways

count_k

count_k解析

count_k例子

paths

max_product

max_product解析

max_product例子

flatten

我的solution

gpt的解法

代码解释

热门标签