哲学问题:CS 61B Fibonacci 数列
重复性过高
我们之前实现的 Fibonacci 数列的代码如下: 下面是java的实现代码
1
2
3
4
5
6
7
8
9
public static long fibOld(int n){
if (n == 0){
return 0;
} else if (n == 1) {
return 1;
} else {
return fibOld(n - 1) + fibOld(n - 2);
}
}
下面是c语言的代码
1
2
3
4
5
6
7
8
9
int fibOld(int num){
if (num == 0){
return 0;
} else if (num == 1){
return 1;
} else {
return fibOld(num - 1) + fibOld(num - 2);
}
}
这个递归实现的斐波那契数列的代码很简单,也很易懂,但是就是会有很大的时间复杂度以及内存。
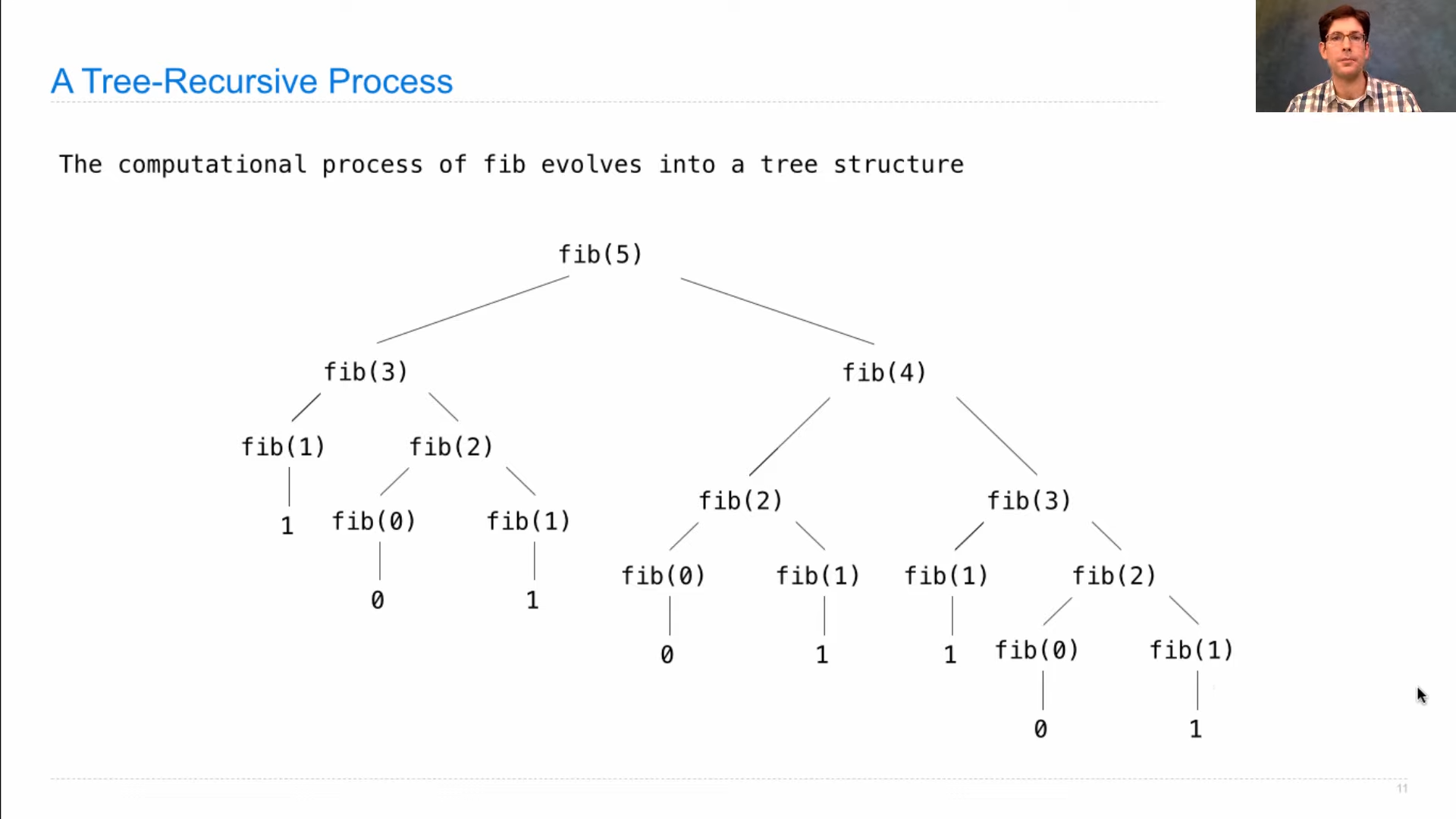
假设我们在计算第fibo(5)的时候,我们需要计算fibo(4)和fibo(3)。
但是在计算第4个数的时候,我们需要计f(3)和f(2)。注意这里的第三个数和一次的第三个数不是同一个数。
但是实际上我们已经计算过一次f(3),我们又重复地计算了一遍f(3)。
具体为什么会重复的完整版介绍,可以看cs61a John的介绍
(如果视频过期了,应该是cs61a更新了新的一年,去找最新的cs61里面”Tree Recursion”对应的list的视频就有了)
以此类推,当我们计算序号很大的数的时候,会有许多数都是重复出现的,我们一直在repeat我们的工作,我们明明已经出来fibo(3)了,但是还是要重新计算很多次fibo(3)。
这样子就导致我们的工作被被浪费了,因为我们没有把我们已经计算出来的结果保存下来!
如果不改进算法的话,计算第50多个数的时候,就会导致计算机卡死。
优化fibo:动态规划
非常简单粗暴的方法
虽然听起来有点高大上
实际上就是拿一个数组将我们前面计算过的元素都保存下来。
首先初始化数组,将a[0],a[1]初始化为0和1,然后从a[2]开始计算。
(改进于copilot)
Java的实现方法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
copilot动态规划的做法,便于理解cs61b老师要求的做法
1.假设要计算i = 10上的fib数列,则定义定义一个长度为11的数组
2.从i = 2开始计算,dp[i] = dp[i - 2] + dp[i - 1]
3.这样子避免了大量的重复计算
4. 开始启动 fib2_helper(10, 0, 1)
*/
public static int fib2_helper(int n, int f0, int f1) {
int [] dp = new int[n+1];
dp[0] = f0;
dp[1] = f1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 2] + dp[i - 1];
}
return dp[n];
}
C语言的实现方法如下:
由于c语言的数组不能够定义一个变量作为数组的长度
所以我们需要用宏定义来定义数组的长度
初始化数组的a[0]和a[1]和0和1,然后再用一个for循环来初始化数组。
1
2
3
4
5
6
7
8
#define n 80
int main() {
int array[n] = {0};
array[0] = 0, array[1] = 1;
for (int i = 2; i < n; ++i) {
array[i] = array[i - 1] + array[i - 1];
}
}
优化fibo:cs61 b的做法
在思考完这个递归问题的时候,我发现这是一个这是一个哲学问题
假设你现在是茫茫斐波那契数列数组中的某一个元素,你不知道前面有多少个人 你也不知道你后面有多少个人, 你只需要知道的是 1. 你要到哪里去 2. 你在哪里,你是否已经走到你要去的地方 3. 你的前一个值是什么 4. 你的值是什么
这样我们就可以写出来一个递归的代码了,相比于一开始的递归函数,这个递归函数需要更多的变量来记录。
1
2
3
4
5
6
7
8
9
10
11
12
13
/** cs61b视频的做法,f1记录的是下一个元素位置的元素的值
n: the steps need to reach
k: the current step
f0: current value
f1: next value
*/
public static int fib2_ucb(int n, int k, int f0, int f1) {
if (k == n){
return f0;
} else {
return fib2_ucb(n , k + 1, f1,f0 + f1);
}
}
如何使用这个函数?
假设我们要计算第5个斐波那契数列的值
我们只需要执行, fib2_ucb(5, 0, 0, 1)
仔细解释一下:用n来记录你需要的需要达到的长度
用k来记录现在你走到了哪里,用f0来记录当前的值,用f1来记录下一个元素的值。
一开始的话fib2_ucb(5, 0, 0, 1),由于f0是0,代表现在的值是1,下一个值是1.
然后进入递归(5, 1, 1, 1),由于k不等于n,所以进入else语句 我们当前元素的值是1,下一个值是1
继续进行(5, 2, 1, 2) 我们当前元素的值是1,下一个值是2
(5, 3, 2, 3) 我们当前元素的值是2,下一个值是3
(5, 4, 3, 5) 我们当前元素的值是3,下一个值是5
(5, 5, 5, 8)
我们当前元素的值是5,下一个值是8
-> 由于此时k已经等于n,结束递归,返回f0,也就是得到f(5)是5
总结一下:把你想象成一个斐波那契数里面的数,你只需要记住4个东西
- 需要达到的步数
- 当前所在的步数
- 你当前的值
- 你的下一个值
这就是这个更加高效的fibonacci递归的实现,不需要每次都重复计算。
只需要记录下你的当前值和下一个值就可以了
在运行改进的代码的时候,可以发现fibonacci计算的速度提升很多倍了。
总结:Don’t repeat yourself ! – John CS61